The 17-point scoring system is a common 8-ball scoring method used in pool leagues. The winner of each game earns 10 points plus one point for each ball his or her opponent has left on the table. The loser of each game earns one point for each ball he or she pockets (i.e. solids or stripes) for a maximum of seven points. The combined score from both players always adds up to 17.
Advantages
Scoring is simple and easy to understand. At the end of each game, the score is quickly determined by the balls left on the table. There is no need to track innings, safeties, or anything else during the game. Players also have an opportunity to earn points for their team even when they lose a game. It's not much fun to play well and make several balls only to get a zero. With the 17-point scoring system, players and teams at least get some credit for their efforts.
Disadvantages
Each player carries an "average" which is considered their rating and is often used for handicapping. This problem is discussed in greater detail below. Another problem is that player averages in different leagues and regions are often not comparable. Finally, situations occasionally occur in which a player's incentive to win the game is replaced with an incentive to just make a few balls.
Advantages
Scoring is simple and easy to understand. At the end of each game, the score is quickly determined by the balls left on the table. There is no need to track innings, safeties, or anything else during the game. Players also have an opportunity to earn points for their team even when they lose a game. It's not much fun to play well and make several balls only to get a zero. With the 17-point scoring system, players and teams at least get some credit for their efforts.
Disadvantages
Each player carries an "average" which is considered their rating and is often used for handicapping. This problem is discussed in greater detail below. Another problem is that player averages in different leagues and regions are often not comparable. Finally, situations occasionally occur in which a player's incentive to win the game is replaced with an incentive to just make a few balls.
The Old Way
Traditionally, each player earns an "average" which is used as a rating. A player's average is the number of points scored divided by the number of games played (Total Points / Total Games) and can range from 0 to 17. For example, if a person scores 389 points over 32 games, he or she will have an average of 12.16 (389/32).
Each team member's average is totaled to establish a team average. When two teams play, the difference in their averages is the handicap. See the below example. Team A has an average of 39.72 and Team B has an average of 54.62. Because Team B's average is 14.9 points higher, Team A would get 14 or 15 points, depending on the league's rounding rules, added to its score in each round as a handicap.
Each team member's average is totaled to establish a team average. When two teams play, the difference in their averages is the handicap. See the below example. Team A has an average of 39.72 and Team B has an average of 54.62. Because Team B's average is 14.9 points higher, Team A would get 14 or 15 points, depending on the league's rounding rules, added to its score in each round as a handicap.
|
TEAM A Player 1 - 6.67 Player 2 - 5.23 Player 3 - 8.12 Player 4 - 7.89 Player 5 - 11.81 Total - 39.72 |
TEAM B Player 1 - 12.16 Player 2 - 10.24 Player 3 - 8.89 Player 4 - 13.35 Player 5 - 9.98 Total - 54.62 |
HANDICAP Team A - 39.72 Team B - 54.62 Difference - 14.9 pts. Handicap: 15 pts. per round |
This approach works reasonably well but it has some flaws. First, a person's average is not always a true reflection of his or her skill level. If a person plays more higher-skilled players, his or her average will tend to be lower. If that same person plays more beginning and social players, his or her average will tend to be higher. It's the same person but a different average depending on the skill level of past competitors.
Another issue is that averages in different leagues and regions are often not comparable. An average of 12.16 in Chicago is probably not the same as an average of 12.16 in Dickinson, Alabama. Because the populations are so different, the talent pool is larger and the overall skill level is likely higher in Chicago.
Another issue is that averages in different leagues and regions are often not comparable. An average of 12.16 in Chicago is probably not the same as an average of 12.16 in Dickinson, Alabama. Because the populations are so different, the talent pool is larger and the overall skill level is likely higher in Chicago.
A Better Way Using FargoRate
FargoRate fixes these problems. Leagues can continue using the 17-point system for scoring while utilizing FargoRate for player ratings and handicapping. Here's how it works.
Instead of having an average, each player has an "expected score" in each game based on the Fargo Ratings of the two players. The expected score for each player is expressed as...
Instead of having an average, each player has an "expected score" in each game based on the Fargo Ratings of the two players. The expected score for each player is expressed as...
EXPECTED SCORE = (Probability of Winning * Winning Score) + (Probability of Losing * Losing Score)
FargoRate already knows the statistical probability of each person winning a game. However, the winning and losing scores are a little complicated because they can vary between zero and 17 and zero and seven respectively. So what do we do? After analyzing lots of data, it turns out that a person's expected losing score is a function of his or her opponent's rating. This is somewhat intuitive...when a person loses to a lower-skilled player, he or she will likely make more balls than in a loss against a higher-skilled player. So, we use this function for the losing score.
Let's look at an example. Suppose Ted has a Fargo Rating of 400 and is playing Robert who has a Fargo Rating of 569. Statistically, Robert has a 76% chance of winning and a 24% chance of losing each game. The losing score function reveals that on average, Robert is expected to score 4.2 points in his losses to Ted. Because the two scores must always equal 17, Ted is expected to score 12.8 (17 pts. - 4.2 pts.) on average when he defeats Robert. The losing score function also reveals that on average, Ted is expected to score, 3.5 points in his losses to Robert. Again, because the two scores must always equal 17, Robert is expected to score 13.5 (17 pts. - 3.5 pts.) on average when he defeats Ted. The total expected scores are as follows.
Let's look at an example. Suppose Ted has a Fargo Rating of 400 and is playing Robert who has a Fargo Rating of 569. Statistically, Robert has a 76% chance of winning and a 24% chance of losing each game. The losing score function reveals that on average, Robert is expected to score 4.2 points in his losses to Ted. Because the two scores must always equal 17, Ted is expected to score 12.8 (17 pts. - 4.2 pts.) on average when he defeats Robert. The losing score function also reveals that on average, Ted is expected to score, 3.5 points in his losses to Robert. Again, because the two scores must always equal 17, Robert is expected to score 13.5 (17 pts. - 3.5 pts.) on average when he defeats Ted. The total expected scores are as follows.
ROBERT (569)Expected Score vs Ted = 11.3 pts. (76% * (17 pts. - 3.5 pts.)) + (24% * 4.2 pts.) |
TED (400)Expected Score vs Robert = 5.7 pts. (24% * (17 pts. - 4.2 pts.)) + (76% * 3.5 pts.) |
This calculation is done for every single game played during a league match. In each round, both team's expected scores are totaled to determine the team's expected score for the round. The difference in the team's expected scores is the handicap for that round.
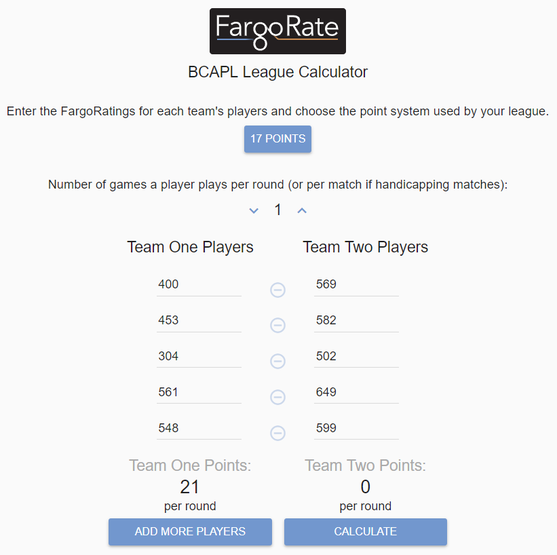
Confused yet? Don't be. FargoRate and LMS can do all the work for you. When using paper score sheets on league night, visit http://leaguecalc.fargorate.com and enter the ratings of each player for the round. See the below example. In this scenario, there are two 5-player teams playing a round robin format where each person plays one game. The result is "Team One" gets a 21-point handicap in the round.
Confused yet? Don't be. FargoRate and LMS can do all the work for you. When using paper score sheets on league night, visit http://leaguecalc.fargorate.com and enter the ratings of each player for the round. See the below example. In this scenario, there are two 5-player teams playing a round robin format where each person plays one game. The result is "Team One" gets a 21-point handicap in the round.
When entering scores in LMS, these calculations are automatic. Additionally, FargoRate is developing an LMS mobile scoring app that will make all of this seamless and allow teams to score matches on their phones or tablets and submit them directly to LMS.
Summary
The 17-point system is great for league play and we can now make it even better. You no longer have to tolerate unreliable averages and inaccurate handicaps. You can keep the advantages of the 17-point scoring system while using FargoRate to make ratings and handicaps more accurate. The result is more competitive leagues with more teams in contention and more players returning session to session.
For more information about how FargoRate and LMS can help your league, contact us at 702-719-POOL (7665).
For more information about how FargoRate and LMS can help your league, contact us at 702-719-POOL (7665).